PROV 1 MA 4 Lösningar
Provet omfattar kap.1-2 och repetition hittar du på
s.43-49 för kap 1
s.89-97 för kap 2
Nedan är uppgifter och lösningarna.
Uppgift
1. Beräkna ur figur.
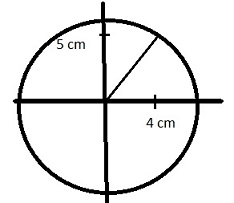
Svar:
1a) sinv=0,78
1b sin ( 180-v) = 0,78
1c cos(90-v)=0,78
2 Ange Amplitud och Period när y= 4- 6sin5x
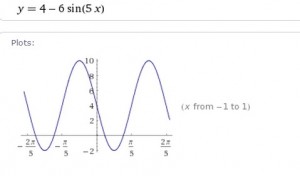
Svar:
Amplitud = 6
Period = 360/5 = 72
3 Beräkna vinkeln v i grader och radianer. När båglängden är 60 cm och radien är 50 cm.
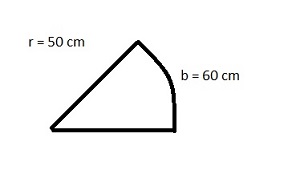
Båglängd= v/360 *2pir ger v= 360*b/ 2pir
v=360*60/2pi*50 = 69 grader.
b= v*r ger v=b/r = 60/50 = 1,2 Svar 69 grader och 1,2
4a)Beräkna derivatan till g(x) = sin5x
(1) g(x)=5x=u g´(x)= 5
(2) f(u)=sinu f´(x)= cos(u)
y`(x) = f´(u)*g´(x)= cosu*5= cos(5x)*5 = 5cos(5x)
4b)h(x)= (2x+1)^5 ger h´(x)= 10(2x+1)^4
4c) f(x)=cos(x^2-5) ger f`(x)= -2xsin(x^2+5)
5) Beräkna cos(0,5x)= -0,68 ( räkna i radianer )
x= +- 4,64 + n*4pi
6) Bevis a, b , c är tre på varandra följande tal.
P tillhör Q
P= a, b, och c
Q=Då är (a^2+b^2+c^2-2)/ 3 ett heltal
Lösn
a=n
b=n+1
c=n+2
n^2+(n+1)^2+(n+2)^2-2 / 3
= n^2+n^2+2n+1+n^2+4n+4-2
=3n^2+6n-3 / 3 = n^2-2n+1
Vilket är samma sak som (n+1)^2 och )N+2)^2 är ett heltal eftersom vi vet att n+1 är ett heltal.
Ett heltal upphöjt till sig själb blir ett nytt heltal.
P tillhör Q VSV,
7. Visa att cos2x/ cosx-sinx = sinx+cosx
Lösning.
cos2x/ cosx-sinx = cos^2(x)-sin^2(x) / cosx-sinx
= (cosx+sinx)*(cosx-sinx)/ cosx-sinx
= cosx+sinx=sinx+cosx = VL VSV
8 Kurvanalys
9) Kurvanalys
A*sink(x+v)+d
10 2cos^2(x) -cosx= 0
cosx(2cosx-1) = 0
x= +-90+n*2pi
x=+-60+n*2pi
11 Analys y= A*sink(t+v) +d