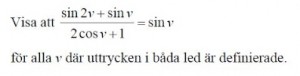2. Trigonometri och grafer
Inledande aktivitet- Läs och gör hela den inledande aktiviteten på s.51 (kapitel 2).
Enkel harmonisk svängning
http://www.animations.physics.unsw.edu.au//jw/SHM.htm
Titta noga vad du ska göra.
Det är två filmer som du ska titta på. Skicka ett mejl till mig om du kör fast på någon uppgift så kan vi gå igenom den senare.
Klicka på bilden och prova!
http://www.georgiostheodoridis.se/archives/MDFunktionerSinCosTan2000V2.html
Källa: Georgios Theodoridis
Läs s.53-54 Trigonometriska kurvor och titta på filmen:
Sinus- och Cosinuskurvan och gör uppgifterna
2102-2104, 2106, 2107, 2110, 2111
Från enhetscirkeln till sinus- och cosinusfunktionen
Ekvationer och förskjutna kurvor
Läs s.56 och 58 och titta på de korta (nåja) filmerna:
Trigonometriska kurvor och ekvationer
Förskjutna kurvor i y-led
Förskjutna kurvor i x-led
Tangens
Läs s.62-63 och titta på filmerna:
Ekvationer med tangens y = tanx
som du hittar HÄR. På lektionen jobbar vi med uppgifterna:
2155, 2156a, 2157a, 2158a, 2159a, 2162, 2164, 2169, 2171, 2174
Ett sista trigonometriskt samband
Läs s.65-66 och titta på filmen:
Kurvan y = a*sinx + b*cosx
Bra uppgifter:
2177, 2179, 2182, 2187
På lektionen kommer vi också att jobba med radianer.
Cirkelsektorn och Radianer
som du hittar HÄR. Bra uppgifter:
2205, 2206, 2208, 2210-2216, 2219
2224, 2227, 2228, 2230, 2232
Utmaning
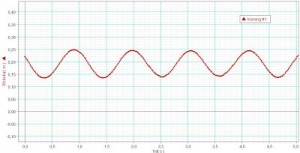
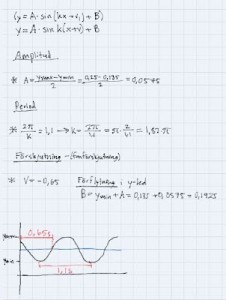
Under filmen hittar du sinuskurvan som beskriver viktens läge. Kan du ange denna kurvas ekvation på formen: y = A*sin k(x + v) + B
Radianer
Läs om radianer på s.68-73 och titta på filmerna:
Radianer
Derivatan av sinx och cosx
Läs s.74-75 och titta på filmerna:
Gränsvärdet för sinx/x
Gränsvärdet för (cosx-1)/x
Derivatan av sinx och cosx
Kedjeregeln – Derivatan av sammansatta funktioner
Gå igenom teorin på s.78-79 och gör uppgifterna 2322-2337.
Tillämpningar och problemlösning
Läs det lösta exemplet på s.80-81 noga och gör sedan uppgifterna:
2403, 2405, 2407, 2409, 2410, 2411, 2413, 2417, 2421
Hur bestämmer man grafens funktion ?
Asymptoter